The Mystery of an Infinite Expression

Mathematics is a treasure trove of intriguing patterns and mind-boggling concepts. Have you ever come across an expression that keeps going forever? Today, we’ll dive into one such fascinating infinite expression and uncover its mystery!

Let’s consider the following infinite expression:

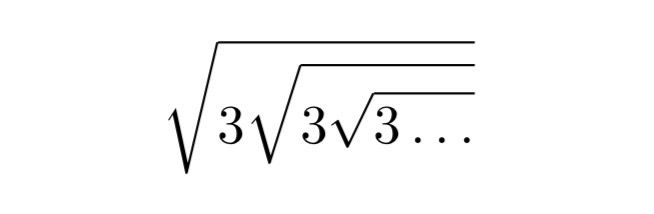
At first glance, this may seem like an endless labyrinth of infinite square roots. But fear not - mathematics has a way of simplifying even the most complex-looking expressions.

Breaking it down

Let’s begin by giving our expression a name. Let’s call it S, as we will be solving this like we have done in the past when proving expressions in Sequences and Series.

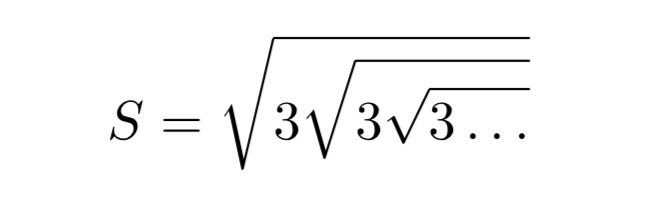
Now that S is defined, let’s think about what options we have. Can you think of a way in which we can manipulate S to help us out? What if we could perform an operation on S, in order to write it in terms of itself?

Let’s try squaring each side of our equation…

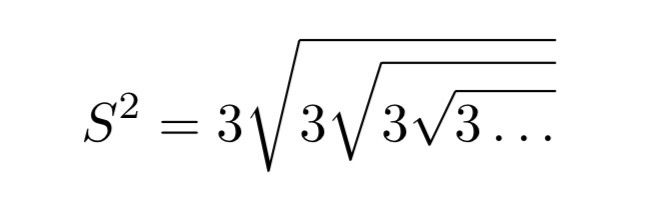
Hopefully, you can see that what we have on the right-hand side is just 3 times our original expression, S. We can therefore simplify this, writing:

This is much better! We have removed any traces of our infinite square roots, leaving a quadratic expression that we are used to. To solve it, we perform the following steps:

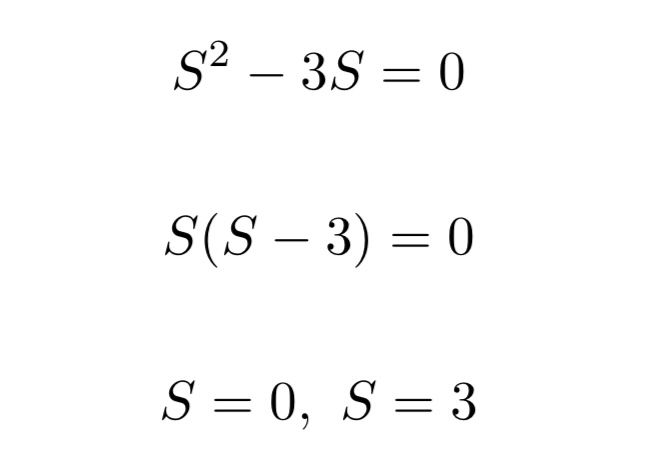
Which of these solutions do you think is correct? It can’t be zero, as we know our answer should be a positive, whole number. Therefore, our answer must be 3.

Try putting this into your calculator for 10 iterations of root 3. How close do you get to 3?

Why Does This Work?

Infinite radicals like this one might seem daunting, but they follow patterns that allow them to converge to a finite value. The key lies in self-referential equations. Despite the long name, this just refers to an equation where a smaller part of the expression mirrors the whole.

Conclusion

And there you have it! The infinite radical evaluates to 3. This is just one example of how seemingly complex expressions can have surprisingly elegant solutions.

Stay curious, keep exploring, and let the wonders of mathematics inspire you!